データ構造

マップ

import qualified Data.Map as Map

kv :: Map.Map Integer String
kv = Map.fromList [(1, "a"), (2, "b")]

lkup :: Integer -> String -> String
lkup key def =
  case Map.lookup key kv of
    Just val -> val
    Nothing  -> def

木

import Data.Tree

{-

   A
  / \
 B   C
    / \
   D   E

-}

tree :: Tree String
tree = Node "A" [Node "B" [], Node "C" [Node "D" [], Node "E" []]]

postorder :: Tree a -> [a]
postorder (Node a ts) = elts ++ [a]
  where elts = concat (map postorder ts)

preorder :: Tree a -> [a]
preorder (Node a ts) = a : elts
  where elts = concat (map preorder ts)

ex1 = drawTree tree
ex2 = drawForest (subForest tree)
ex3 = flatten tree
ex4 = levels tree
ex5 = preorder tree
ex6 = postorder tree

Set

import qualified Data.Set as Set

set :: Set.Set Integer
set = Set.fromList [1..1000]

memtest :: Integer -> Bool
memtest elt = Set.member elt set

Vector

Vectors are high performance single dimensional arrays that come come in six variants, two for each of the following types of a mutable and an immutable variant.

• Data.Vector
• Data.Vector.Storable
• Data.Vector.Unboxed

The most notable feature of vectors is constant time memory access with ((!)) as well as variety of efficient map, fold and scan operations on top of a fusion framework that generates surprisingly optimal code.

fromList :: [a] -> Vector a
toList :: Vector a -> [a]
(!) :: Vector a -> Int -> a
map :: (a -> b) -> Vector a -> Vector b
foldl :: (a -> b -> a) -> a -> Vector b -> a
scanl :: (a -> b -> a) -> a -> Vector b -> Vector a
zipWith :: (a -> b -> c) -> Vector a -> Vector b -> Vector c
iterateN :: Int -> (a -> a) -> a -> Vector a

import Data.Vector.Unboxed as V

norm ::  Vector Double -> Double
norm = sqrt . V.sum . V.map (\x -> x*x)

example1 :: Double
example1 = norm $ V.iterateN 100000000 (+1) 0.0

See: Numerical Haskell: A Vector Tutorial

可変Vector

freeze :: MVector (PrimState m) a -> m (Vector a)
thaw :: Vector a -> MVector (PrimState m) a

Within the IO monad we can perform arbitrary read and writes on the mutable vector with constant time reads and writes. When needed a static Vector can be created to/from the MVector using the freeze/thaw functions.

import GHC.Prim
import Control.Monad
import Control.Monad.ST
import Control.Monad.Primitive

import Data.Vector.Unboxed (freeze)
import Data.Vector.Unboxed.Mutable
import qualified Data.Vector.Unboxed as V

example :: PrimMonad m => m (V.Vector Int)
example = do
  v <- new 10
  forM_ [0..9] $ \i ->
     write v i (2*i)
  freeze v

-- vector computation in IO
vecIO :: IO (V.Vector Int)
vecIO = example

-- vector computation in ST
vecST :: ST s (V.Vector Int)
vecST = example


main :: IO ()
main = do
  vecIO >>= print
  print $ runST vecST

非整序コンテナ

fromList :: (Eq k, Hashable k) => [(k, v)] -> HashMap k v
lookup :: (Eq k, Hashable k) => k -> HashMap k v -> Maybe v
insert :: (Eq k, Hashable k) => k -> v -> HashMap k v -> HashMap k v

Both the HashMap and HashSet are purely functional data structures that are drop in replacements for the containers equivalents but with more efficient space and time performance. Additionally all stored elements must have a Hashable instance.

import qualified Data.HashSet as S
import qualified Data.HashMap.Lazy as M

example1 :: M.HashMap Int Char
example1 = M.fromList $ zip [1..10] ['a'..]

example2 :: S.HashSet Int
example2 = S.fromList [1..10]

See: Johan Tibell: Announcing Unordered Containers

ハッシュテーブル

Hashtables provides hashtables with efficient lookup within the ST or IO monad.

import Prelude hiding (lookup)

import Control.Monad.ST
import Data.HashTable.ST.Basic

-- Hashtable parameterized by ST "thread"
type HT s = HashTable s String String

set :: ST s (HT s)
set = do
  ht <- new
  insert ht "key" "value1"
  return ht

get :: HT s -> ST s (Maybe String)
get ht = do
  val <- lookup ht "key"
  return val

example :: Maybe String
example = runST (set >>= get)

new :: ST s (HashTable s k v)
insert :: (Eq k, Hashable k) => HashTable s k v -> k -> v -> ST s ()
lookup :: (Eq k, Hashable k) => HashTable s k v -> k -> ST s (Maybe v)

グラフ

The Graph module in the containers library is a somewhat antiquated API for working with directed graphs. A little bit of data wrapping makes it a little more straightforward to use. The library is not necessarily well-suited for large graph-theoretic operations but is perfectly fine for example, to use in a typechecker which need to resolve strongly connected components of the module definition graph.

import Data.Tree
import Data.Graph

data Grph node key = Grph
  { _graph :: Graph
  , _vertices :: Vertex -> (node, key, [key])
  }

fromList :: Ord key => [(node, key, [key])] -> Grph node key
fromList = uncurry Grph . graphFromEdges'

vertexLabels :: Functor f => Grph b t -> (f Vertex) -> f b
vertexLabels g = fmap (vertexLabel g)

vertexLabel :: Grph b t -> Vertex -> b
vertexLabel g = (\(vi, _, _) -> vi) . (_vertices g)

-- Topologically sort graph
topo' :: Grph node key -> [node]
topo' g = vertexLabels g $ topSort (_graph g)

-- Strongly connected components of graph
scc' :: Grph node key -> [[node]]
scc' g = fmap (vertexLabels g . flatten) $ scc (_graph g)

So for example we can construct a simple graph:

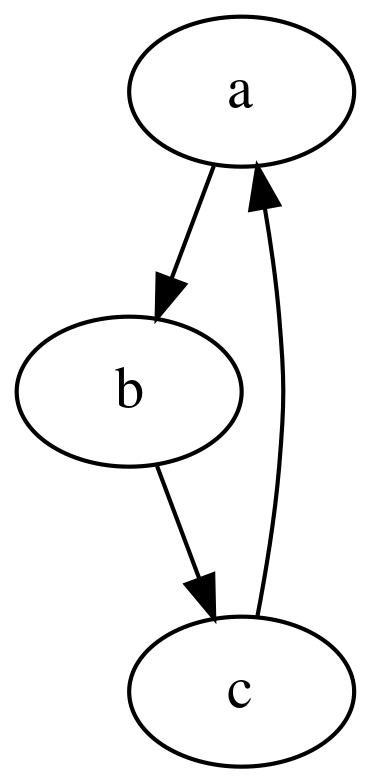
ex1 :: [(String, String, [String])]
ex1 = [
    ("a","a",["b"]),
    ("b","b",["c"]),
    ("c","c",["a"])
  ]

ts1 :: [String]
ts1 = topo' (fromList ex1)
-- ["a","b","c"]

sc1 :: [[String]]
sc1 = scc' (fromList ex1)
-- [["a","b","c"]]

Or with two strongly connected subgraphs:

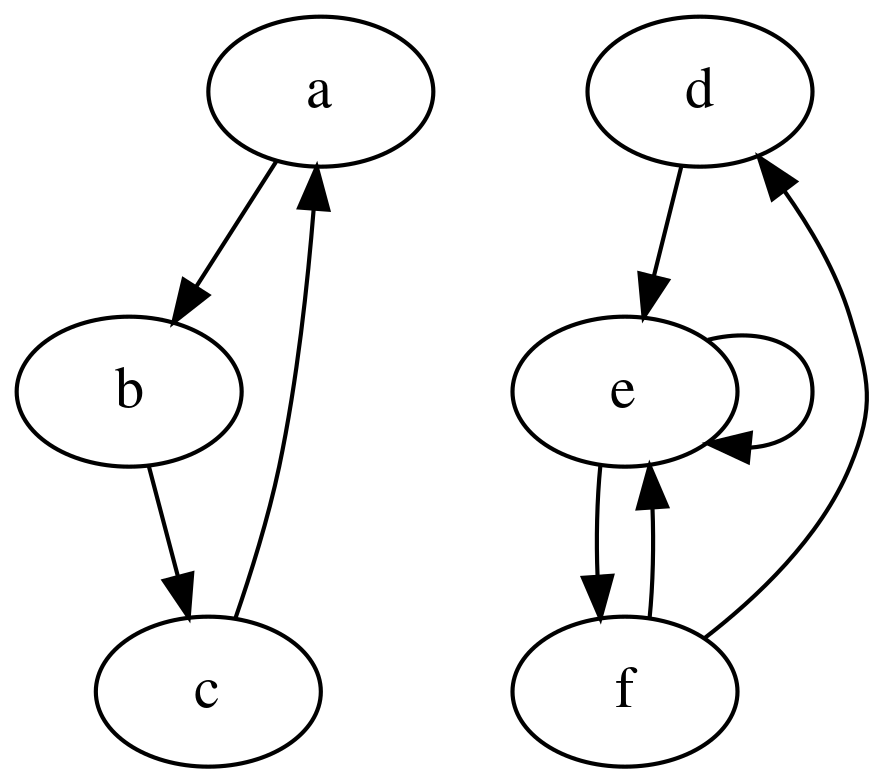
ex2 :: [(String, String, [String])]
ex2 = [
    ("a","a",["b"]),
    ("b","b",["c"]),
    ("c","c",["a"]),

    ("d","d",["e"]),
    ("e","e",["f", "e"]),
    ("f","f",["d", "e"])
  ]


ts2 :: [String]
ts2 = topo' (fromList ex2)
-- ["d","e","f","a","b","c"]

sc2 :: [[String]]
sc2 = scc' (fromList ex2)
-- [["d","e","f"],["a","b","c"]]

See: GraphSCC

グラフ理論

The fgl library provides are more efficient graph structure and a wide variety of common graph-theoretic operations. For example calculating the dominance frontier of a graph shows up quite frequently in control flow analysis for compiler design.

import qualified Data.Graph.Inductive as G

cyc3 :: G.Gr Char String
cyc3 = G.buildGr
       [([("ca",3)],1,'a',[("ab",2)]),
                ([],2,'b',[("bc",3)]),
                ([],3,'c',[])]

-- Loop query
ex1 :: Bool
ex1 = G.hasLoop x

-- Dominators
ex2 :: [(G.Node, [G.Node])]
ex2 = G.dom x 0

x :: G.Gr Int ()
x = G.insEdges edges gr
  where
  gr = G.insNodes nodes G.empty
  edges = [(0,1,()), (0,2,()), (2,1,()), (2,3,())]
  nodes = zip [0,1 ..] [2,3,4,1]

DList

A dlist is a list-like structure that is optimized for O(1) append operations, internally it uses a Church encoding of the list structure. It is specifically suited for operations which are append-only and need only access it when manifesting the entire structure. It is particularly well-suited for use in the Writer monad.

import Data.DList
import Control.Monad
import Control.Monad.Writer

logger :: Writer (DList Int) ()
logger = replicateM_ 100000 $ tell (singleton 0)

シーケンス

The sequence data structure behaves structurally similar to list but is optimized for append/prepend operations and traversal.

import Data.Sequence

a :: Seq Int
a = fromList [1,2,3]

a0 :: Seq Int
a0 = a |> 4
-- [1,2,3,4]

a1 :: Seq Int
a1 = 0 <| a
-- [0,1,2,3]

行列とHBlas

Just as in C when working with n-dimensional matrices we'll typically overlay the high-level matrix structure onto an unboxed contiguous block of memory with index functions which perform the coordinate translations to calculate offsets. The two most common layouts are:

• Row-major order
• Column-major order

Which are best illustrated.

The calculations have a particularly nice implementation in Haskell in terms of scans over indices.

import qualified Data.Vector as V

data Order = RowMajor | ColMajor

rowMajor :: [Int] -> [Int]
rowMajor = scanr (*) 1 . tail

colMajor :: [Int] -> [Int]
colMajor = init . scanl (*) 1

data Matrix a = Matrix
  { _dims  :: [Int]
  , _elts  :: V.Vector a
  , _order :: Order
  }

fromList :: [Int] -> Order -> [a] -> Matrix a
fromList sh order elts =
  if product sh == length elts
  then Matrix sh (V.fromList elts) order
  else error "dimensions don't match"

indexTo :: [Int] -> Matrix a -> a
indexTo ix mat = boundsCheck offset
  where
    boundsCheck n =
      if 0 <= n && n < V.length (_elts mat)
      then V.unsafeIndex (_elts mat) offset
      else error "out of bounds"
    ordering = case _order mat of
      RowMajor -> rowMajor
      ColMajor -> colMajor
    offset = sum $ zipWith (*) ix (ordering (_dims mat))

matrix :: Order -> Matrix Int
matrix order = fromList [4,4] order [1..16]

ex1 :: [Int]
ex1 = rowMajor [1,2,3,4]
-- [24,12,4,1]

ex2 :: [Int]
ex2 = colMajor [1,2,3,4]
-- [1,1,2,6]

ex3 :: Int
ex3 = indexTo [1,3] (matrix RowMajor)
-- 8

ex4 :: Int
ex4 = indexTo [1,3] (matrix ColMajor)
-- 14

Unboxed matrices of this type can also be passed to C or Fortran libraries such BLAS or LAPACK linear algebra libraries. The hblas package wraps many of these routines and forms the low-level wrappers for higher level-libraries that need access to these foreign routines.

For example the dgemm routine takes two pointers to a sequence of double values of two matrices of size (m × k) and (k × n) and performs efficient matrix multiplication writing the resulting data through a pointer to a (m × n) matrix.

import Foreign.Storable
import Numerical.HBLAS.BLAS
import Numerical.HBLAS.MatrixTypes

-- Generate the constant mutable square matrix of the given type and dimensions.
constMatrix :: Storable a => Int -> a -> IO (IODenseMatrix Row a)
constMatrix n k = generateMutableDenseMatrix SRow (n,n) (const k)

example_dgemm :: IO ()
example_dgemm = do
    left  <- constMatrix 2 (2 :: Double)
    right <- constMatrix 2 (3 :: Double)
    out   <- constMatrix 2 (0 :: Double)

    dgemm NoTranspose NoTranspose 1.0 1.0 left right out

    resulting <- mutableVectorToList $ _bufferDenMutMat out
    print resulting

See: hblas