数学
数値の塔
Haskell の数値の塔は変なので、初心者には混乱の種になっています。Haskell は、他の言語にしばしば見られる”型強制”の仕組みを使わずに、静的型付けでオーバーロードされたリテラルを組み込んでいる、数少ない言語の一つなのです。
さらに混乱させるのは、Haskell の数値リテラルが数値の型クラスにある関数へと脱糖衣されるということです。この関数は、Num や Fractorial 型クラスの任意のインスタンスへと実体化することのできる、多相的な値を呼び出し場所で生み出します。どのインスタンスになるかは推論された型に依ります。
大ざっぱなたとえ話をすれば、私たちは実質的にオブジェクトを穴に入れていて、穴の大きさや形が入れるオブジェクトを定めている、ということです。これはほかの言語と大きく異なります。Haskell 以外では、2.718 のような数値リテラルはコンパイラで特定の型(double か何か)の値へと固定されてしまい、実行時に必要に応じてより狭い、あるいは広い型へとキャストすることになります。
42 :: Num a => a
fromInteger (42 :: Integer)
2.71 :: Fractional a => a
fromRational (2.71 :: Rational)
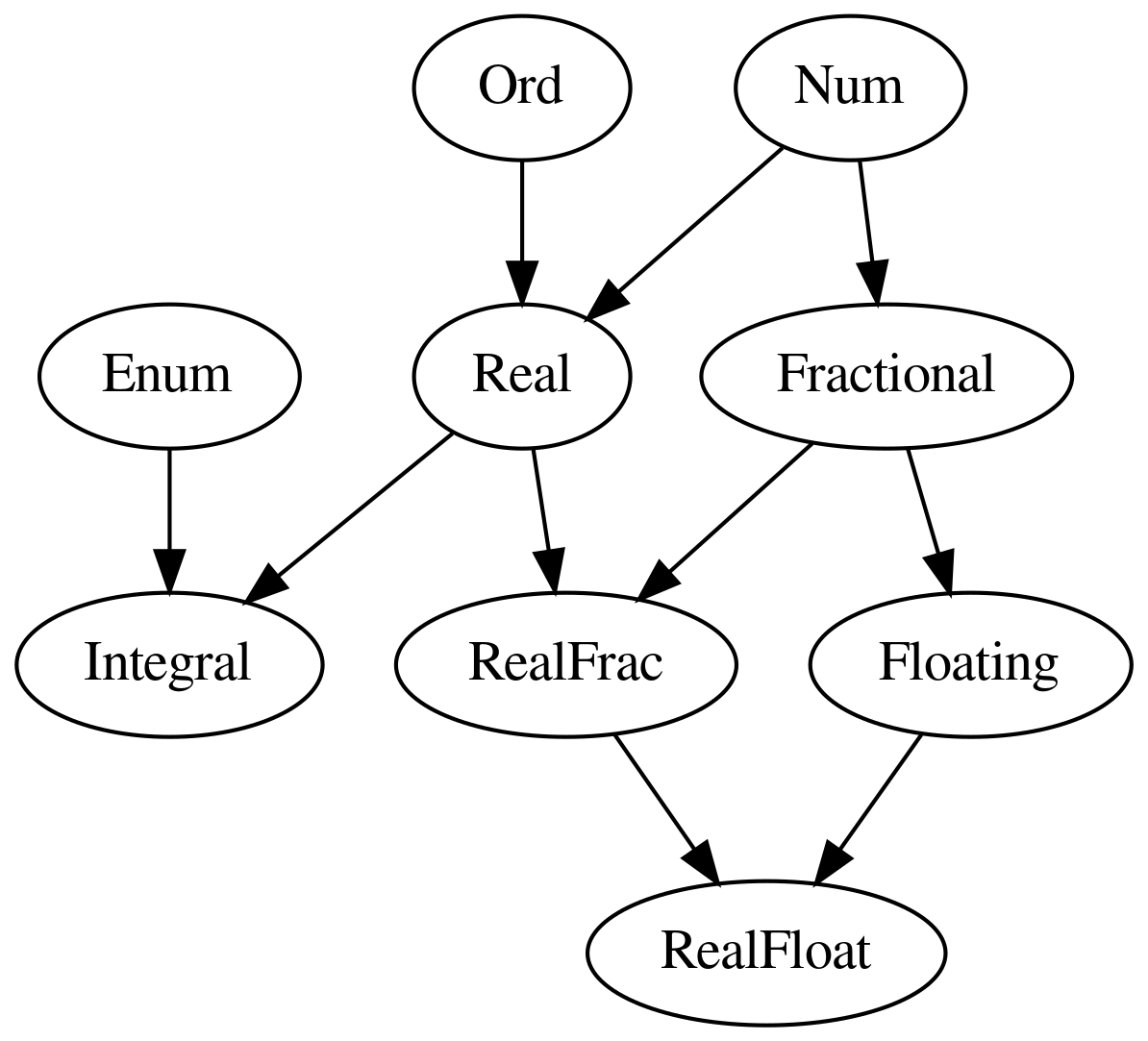
数値の型クラスの階層は以下のように定義されています。
class Num a
class (Num a, Ord a) => Real
class Num a => Fractional a
class (Real a, Enum a) => Integral a
class (Real a, Fractional a) => RealFrac a
class Fractional a => Floating a
class (RealFrac a, Floating a) => RealFloat a
具体的な数値型の間の変換(変換元:左の列、変換先:上の行)はいくつかの総称関数で実現できます。
| Double | Float | Int | Word | Integer | Rational | |
|---|---|---|---|---|---|---|
| Double | id | fromRational | truncate | truncate | truncate | toRational |
| Float | fromRational | id | truncate | truncate | truncate | toRational |
| Int | fromIntegral | fromIntegral | id | fromIntegral | fromIntegral | fromIntegral |
| Word | fromIntegral | fromIntegral | fromIntegral | id | fromIntegral | fromIntegral |
| Integer | fromIntegral | fromIntegral | fromIntegral | fromIntegral | id | fromIntegral |
| Rational | fromRatoinal | fromRational | truncate | truncate | truncate | id |
整数
GHC の Integer 型は GMP (libgmp) の任意精度算術ライブラリにより実装されています。Int 型と異なり、Integer の値の大きさは使えるメモリだけにより決まります。注目すべきなのは、libgmp は Haskell のコンパイルされたバイナリが動的にリンクしている数少ないライブラリであるということです。
代替のライブラリ integer-simple を libgmp の代わりにリンクすることもできます。
参照:
複素数
Haskell では Complex[複素数]データ型を使って複素数を使えます。第一引数が実部、第二引数が虚部です。
-- 1 + 2i
let complex = 1 :+ 2
data Complex a = a :+ a
mkPolar :: RealFloat a => a -> a -> Complex a
Complex の Num インスタンスは Complex の引数が RealFloat のインスタンスである場合に限り定義されます。
λ: 0 :+ 1
0 :+ 1 :: Complex Integer
λ: (0 :+ 1) + (1 :+ 0)
1.0 :+ 1.0 :: Complex Integer
λ: exp (0 :+ 2 * pi)
1.0 :+ (-2.4492935982947064e-16) :: Complex Double
λ: mkPolar 1 (2*pi)
1.0 :+ (-2.4492935982947064e-16) :: Complex Double
λ: let f x n = (cos x :+ sin x)^n
λ: let g x n = cos (n*x) :+ sin (n*x)
Scientific
scientific :: Integer -> Int -> Scientific
fromFloatDigits :: RealFloat a => a -> Scientific
scientific は科学記法を使って表される任意精度の数値をサポートしています。コンストラクタは任意の大きさを取れる Integer の引数を仮数部に受け取り、指数部に Int を受け取ります。その他にも、String からパースしたり Double や Float から型強制したりして値を得ることもできます。
import Data.Scientific
c, h, g, a, k :: Scientific
c = scientific 299792458 (0) -- 光速
h = scientific 662606957 (-42) -- プランク定数
g = scientific 667384 (-16) -- 重力定数
a = scientific 729735257 (-11) -- 微細構造定数
k = scientific 268545200 (-9) -- ヒンチン定数
tau :: Scientific
tau = fromFloatDigits (2*pi)
maxDouble64 :: Double
maxDouble64 = read "1.7976931348623159e308"
-- Infinity
maxScientific :: Scientific
maxScientific = read "1.7976931348623159e308"
-- 1.7976931348623159e308
統計
import Data.Vector
import Statistics.Sample
import Statistics.Distribution.Normal
import Statistics.Distribution.Poisson
import qualified Statistics.Distribution as S
s1 :: Vector Double
s1 = fromList [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
s2 :: PoissonDistribution
s2 = poisson 2.5
s3 :: NormalDistribution
s3 = normalDistr mean stdDev
where
mean = 1
stdDev = 1
descriptive = do
print $ range s1
-- 9.0
print $ mean s1
-- 5.5
print $ stdDev s1
-- 3.0276503540974917
print $ variance s1
-- 8.25
print $ harmonicMean s1
-- 3.414171521474055
print $ geometricMean s1
-- 4.5287286881167645
discrete = do
print $ S.cumulative s2 0
-- 8.208499862389884e-2
print $ S.mean s2
-- 2.5
print $ S.variance s2
-- 2.5
print $ S.stdDev s2
-- 1.5811388300841898
continuous = do
print $ S.cumulative s3 0
-- 0.15865525393145707
print $ S.quantile s3 0.5
-- 1.0
print $ S.density s3 0
-- 0.24197072451914334
print $ S.mean s3
-- 1.0
print $ S.variance s3
-- 1.0
print $ S.stdDev s3
-- 1.0
構成的実数
有限精度浮動小数の実数を使う代わりに、代数関数や超越関数のような演算を行う際に、中間の計算を行う時も精度が失われないように、式の冪級数展開を内部的に操作してくれる Num のインスタンスを使うこともできます。その後は、項を一定の個数だけ削り取って、結果の値を好きな精度へと丸めればよいのです。このアプローチを使うには、制限や但し書き(特に項が発散する可能性があるということ)が付いてきます。それでも、実用上はかなり上手く行きます。
exp(x) = 1 + x + 1/2*x^2 + 1/6*x^3 + 1/24*x^4 + 1/120*x^5 ...
sqrt(1+x) = 1 + 1/2*x - 1/8*x^2 + 1/16*x^3 - 5/128*x^4 + 7/256*x^5 ...
atan(x) = x - 1/3*x^3 + 1/5*x^5 - 1/7*x^7 + 1/9*x^9 - 1/11*x^11 ...
pi = 16 * atan (1/5) - 4 * atan (1/239)
import Data.Number.CReal
-- 代数的
phi :: CReal
phi = (1 + sqrt 5) / 2
-- 超越的
ramanujan :: CReal
ramanujan = exp (pi * sqrt 163)
main :: IO ()
main = do
putStrLn $ showCReal 30 pi
-- 3.141592653589793238462643383279
putStrLn $ showCReal 30 phi
-- 1.618033988749894848204586834366
putStrLn $ showCReal 15 ramanujan
-- 262537412640768743.99999999999925
SATソルバ
充足可能性問題として知られるいくつかの制約に関する問題が、型検査からパッケージ管理までにわたる幅広い分野で現れます。簡単に言えば、充足可能性問題とはいくつかの変数の論理積・論理和の組み合わせからなる文に対して解を求める問題なのです。例えば:
(A v ¬B v C) ∧ (B v D v E) ∧ (D v F)
picosatライブラリを使ってこれを解く場合、ニルで終わる整数のリストとして書いて、数を変数に対応付けるソルバに渡します。
1 -2 3 -- (A v ¬B v C)
2 4 5 -- (B v D v E)
4 6 -- (D v F)
import Picosat
main :: IO [Int]
main = do
solve [[1, -2, 3], [2,4,5], [4,6]]
-- Solution [1,-2,3,4,5,6]
このSATソルバ自体は何百万もの変数を持つこの形式の充足可能性問題を解くことができますし、上手く動作するようによく調整されています。
参照:
SMTソルバ
SAT の問題を一般化して他の理論の述語も扱えるようにしようとすることで、「充足可能性モジュロ理論」(Satisfiability Modulo Theory, SMT) という非常に高度な研究領域が生まれました。既存の SMT ソルバは非常に精巧なプロジェクトであり(たいてい大組織から資金援助を受けていて)、呼び出すにはたいてい他言語関数インターフェースや SMT-lib と呼ばれる共通のインターフェースを使う必要があります。Haskell で最も良く使われている 2 つは、スタンフォード大学の cvc4 とマイクロソフトリサーチの z3 です。
SBVライブラリは様々な SMTソルバを抽象化して、Haskellの組み込みドメイン固有言語で問題を表現して、問題を解く仕事をサードパーティのライブラリに任せられるようにしてくれます。
TODO: SBV について書く
参照: