テスト

はじめに

多くの誤った情報が流れていますが、Haskell でユニットテスト (unit testing) はかなり一般的ですし、十分堅牢です。しかし大まかに言ってユニットテストは Haskell ではあまり重要視されません。型システムにより、尋常でない量の無効なプログラムが、構成的な手法で完全に表現不可能になっているからです。ユニットテストは、開発のライフサイクルの後の方で書かれる傾向があり、一般には表面上の仕組みではなくプログラムの中核の論理について行われることが多いです。

Haskell のライブラリの設計の中で優れた流派の多くは、強力な等式の法則を基盤にプログラムを構成するのを好みます。これにより、プログラムの振る舞いについて、合成しても不変である条件をきちんと保証できるからです。テストのツールの多くがこの流儀の設計に合うように作られています。

QuickCheck

おそらくもっとも有名な Haskell ライブラリであろう QuickCheck は、巨大なランダムなテストを任意の関数に対して引数の型に基づき自動的に生成する、テストのためのフレームワークです。

quickCheck :: Testable prop => prop -> IO ()
(==>) :: Testable prop => Bool -> prop -> Property
forAll :: (Show a, Testable prop) => Gen a -> (a -> prop) -> Property
choose :: Random a => (a, a) -> Gen a

import Test.QuickCheck

qsort :: [Int] -> [Int]
qsort []     = []
qsort (x:xs) = qsort lhs ++ [x] ++ qsort rhs
    where lhs = filter  (< x) xs
          rhs = filter (>= x) xs

prop_maximum ::  [Int] -> Property
prop_maximum xs = not (null xs) ==>
                  last (qsort xs) == maximum xs

main :: IO ()
main = quickCheck prop_maximum

$ runhaskell qcheck.hs
*** Failed! Falsifiable (after 3 tests and 4 shrinks):
[0]
[1]

$ runhaskell qcheck.hs
+++ OK, passed 1000 tests.

テストデータのジェネレータは、ユーザー定義の型に拡張して、テストケースの領域を制限するための条件を指定することができます。

import Test.QuickCheck

data Color = Red | Green | Blue deriving Show

instance Arbitrary Color where
  arbitrary = do
    n <- choose (0,2) :: Gen Int
    return $ case n of
      0 -> Red
      1 -> Green
      2 -> Blue

example1 :: IO [Color]
example1 = sample' arbitrary
-- [Red,Green,Red,Blue,Red,Red,Red,Blue,Green,Red,Red]

参照：

• QuickCheck: An Automatic Testing Tool for Haskell

SmallCheck

QuickCheck と同様、SmallCheck は性質をテストするシステムですが、ランダムな恣意的なテストデータを生成する代わりに、固定された深さのテストデータの決定論的な列で順に確かめていきます。

smallCheck :: Testable IO a => Depth -> a -> IO ()
list :: Depth -> Series Identity a -> [a]
sample' :: Gen a -> IO [a]

λ: list 3 series :: [Int]
[0,1,-1,2,-2,3,-3]

λ: list 3 series :: [Double]
[0.0,1.0,-1.0,2.0,0.5,-2.0,4.0,0.25,-0.5,-4.0,-0.25]

λ: list 3 series :: [(Int, String)]
[(0,""),(1,""),(0,"a"),(-1,""),(0,"b"),(1,"a"),(2,""),(1,"b"),(-1,"a"),(-2,""),(-1,"b"),(2,"a"),(-2,"a"),(2,"b"),(-2,"b")]

これは、プログラムのすべてのありうる入力をある深さまで生成するのに便利です。

import Test.SmallCheck

distrib :: Int -> Int -> Int -> Bool
distrib a b c = a * (b + c) == a * b + a * c

cauchy :: [Double] -> [Double] -> Bool
cauchy xs ys = (abs (dot xs ys))^2 <= (dot xs xs) * (dot ys ys)

failure :: [Double] -> [Double] -> Bool
failure xs ys = abs (dot xs ys) <= (dot xs xs) * (dot ys ys)

dot :: Num a => [a] -> [a] -> a
dot xs ys = sum (zipWith (*) xs ys)

main :: IO ()
main = do
  putStrLn "Testing distributivity..."
  smallCheck 25 distrib

  putStrLn "Testing Cauchy-Schwarz..."
  smallCheck 4 cauchy

  putStrLn "Testing invalid Cauchy-Schwarz..."
  smallCheck 4 failure

$ runhaskell smallcheck.hs
Testing distributivity...
Completed 132651 tests without failure.

Testing Cauchy-Schwarz...
Completed 27556 tests without failure.

Testing invalid Cauchy-Schwarz...
Failed test no. 349.
there exist [1.0] [0.5] such that
  condition is false

QuickCheck と同様に、ユーザー定義のデータ型に対して series のインスタンスを実装することができます。例えば、Vector に対するデフォルトのインスタンスは無いので、実装してみましょう。

{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE MultiParamTypeClasses #-}

import Test.SmallCheck
import Test.SmallCheck.Series
import Control.Applicative

import qualified Data.Vector as V

dot :: Num a => V.Vector a -> V.Vector a -> a
dot xs ys = V.sum (V.zipWith (*) xs ys)

cauchy :: V.Vector Double -> V.Vector Double -> Bool
cauchy xs ys = (abs (dot xs ys))^2 <= (dot xs xs) * (dot ys ys)

instance (Serial m a, Monad m) => Serial m (V.Vector a) where
  series = V.fromList <$> series

main :: IO ()
main = smallCheck 4 cauchy

SmallCheck で Generics を使えば、Serial のインスタンスを導出することもできます。例えば、特定の深さまでのすべての木を列挙するには、こうすることもできます。

{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE DeriveGeneric #-}

import GHC.Generics
import Test.SmallCheck.Series

data Tree a = Null | Fork (Tree a) a (Tree a)
    deriving (Show, Generic)

instance Serial m a => Serial m (Tree a)

example :: [Tree ()]
example = list 3 series

main = print example

QuickSpec

QuickCheck の任意の構造を使うことで、少し意外かもしれませんが、関数の組み合わせをたくさん列挙して、小さいケースに対して入力を検査することで、代数的法則の推論を試みることもできます。

もちろん、このアプローチの根本的な限界は、関数は小さいケースに対してはいかなる興味深い性質も見せないかもしれないということです。ですから、一般にはこのアプローチが機能するとは限りませんが、実用上はかなり有用です。

{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE ConstraintKinds #-}
{-# LANGUAGE ScopedTypeVariables #-}

import Data.List
import Data.Typeable

import Test.QuickSpec hiding (lists, bools, arith)
import Test.QuickCheck

type Var k a = (Typeable a, Arbitrary a, CoArbitrary a, k a)

listCons :: forall a. Var Ord a => a -> Sig
listCons a = background
  [
    "[]"      `fun0` ([]      :: [a]),
    ":"       `fun2` ((:)     :: a -> [a] -> [a])
  ]

lists :: forall a. Var Ord a => a -> [Sig]
lists a =
  [
    -- 任意の変数を表示するための名前
    funs',
    funvars',
    vars',

    -- 周縁的な定義
    listCons a,

    -- 性質を推論する式
    "sort"     `fun1` (sort    :: [a] -> [a]),
    "map"      `fun2` (map     :: (a -> a) -> [a] -> [a]),
    "id"       `fun1` (id      :: [a] -> [a]),
    "reverse"  `fun1` (reverse :: [a] -> [a]),
    "minimum"  `fun1` (minimum :: [a] -> a),
    "length"   `fun1` (length  :: [a] -> Int),
    "++"       `fun2` ((++)    :: [a] -> [a] -> [a])
  ]

  where
    funs'    = funs (undefined :: a)
    funvars' = vars ["f", "g", "h"] (undefined :: a -> a)
    vars'    = ["xs", "ys", "zs"] `vars` (undefined :: [a])


tvar :: A
tvar = undefined

main :: IO ()
main = quickSpec (lists tvar)

これを実行すると、実際にはリストの関数の法則のほとんどを推論することが出来るということが見て取れます。

$ runhaskell src/quickspec.hs
== API ==
-- functions --
map :: (A -> A) -> [A] -> [A]
minimum :: [A] -> A
(++) :: [A] -> [A] -> [A]
length :: [A] -> Int
sort, id, reverse :: [A] -> [A]

-- background functions --
id :: A -> A
(:) :: A -> [A] -> [A]
(.) :: (A -> A) -> (A -> A) -> A -> A
[] :: [A]

-- variables --
f, g, h :: A -> A
xs, ys, zs :: [A]

-- the following types are using non-standard equality --
A -> A

-- WARNING: there are no variables of the following types; consider adding some --
A

== Testing ==
Depth 1: 12 terms, 4 tests, 24 evaluations, 12 classes, 0 raw equations.
Depth 2: 80 terms, 500 tests, 18673 evaluations, 52 classes, 28 raw equations.
Depth 3: 1553 terms, 500 tests, 255056 evaluations, 1234 classes, 319 raw equations.
319 raw equations; 1234 terms in universe.

== Equations about map ==
  1: map f [] == []
  2: map id xs == xs
  3: map (f.g) xs == map f (map g xs)

== Equations about minimum ==
  4: minimum [] == undefined

== Equations about (++) ==
  5: xs++[] == xs
  6: []++xs == xs
  7: (xs++ys)++zs == xs++(ys++zs)

== Equations about sort ==
  8: sort [] == []
  9: sort (sort xs) == sort xs

== Equations about id ==
 10: id xs == xs

== Equations about reverse ==
 11: reverse [] == []
 12: reverse (reverse xs) == xs

== Equations about several functions ==
 13: minimum (xs++ys) == minimum (ys++xs)
 14: length (map f xs) == length xs
 15: length (xs++ys) == length (ys++xs)
 16: sort (xs++ys) == sort (ys++xs)
 17: map f (reverse xs) == reverse (map f xs)
 18: minimum (sort xs) == minimum xs
 19: minimum (reverse xs) == minimum xs
 20: minimum (xs++xs) == minimum xs
 21: length (sort xs) == length xs
 22: length (reverse xs) == length xs
 23: sort (reverse xs) == sort xs
 24: map f xs++map f ys == map f (xs++ys)
 25: reverse xs++reverse ys == reverse (ys++xs)

驚くべきことに、これらはすべて型の情報だけから自動的に推論されたのです！

criterion

criterion は統計的にきちんとしたベンチマークを行うためのツールです。

whnf :: (a -> b) -> a -> Pure
nf :: NFData b => (a -> b) -> a -> Pure
nfIO :: NFData a => IO a -> IO ()
bench :: Benchmarkable b => String -> b -> Benchmark

import Criterion.Main
import Criterion.Config

-- フィボナッチ数に対する愚直な再帰
fib1 :: Int -> Int
fib1 0 = 0
fib1 1 = 1
fib1 n = fib1 (n-1) + fib1 (n-2)

-- フィボナッチ数に対するド・モアブルの閉じた (closed-form) 定義
fib2 :: Int -> Int
fib2 x = truncate $ ( 1 / sqrt 5 ) * ( phi ^ x - psi ^ x )
  where
      phi = ( 1 + sqrt 5 ) / 2
      psi = ( 1 - sqrt 5 ) / 2

suite :: [Benchmark]
suite = [
    bgroup "naive" [
      bench "fib 10" $ whnf fib1 5
    , bench "fib 20" $ whnf fib1 10
    ],
    bgroup "de moivre" [
      bench "fib 10" $ whnf fib2 5
    , bench "fib 20" $ whnf fib2 10
    ]
  ]

main :: IO ()
main = defaultMain suite

$ runhaskell criterion.hs
warming up
estimating clock resolution...
mean is 2.349801 us (320001 iterations)
found 1788 outliers among 319999 samples (0.6%)
  1373 (0.4%) high severe
estimating cost of a clock call...
mean is 65.52118 ns (23 iterations)
found 1 outliers among 23 samples (4.3%)
  1 (4.3%) high severe

benchmarking naive/fib 10
mean: 9.903067 us, lb 9.885143 us, ub 9.924404 us, ci 0.950
std dev: 100.4508 ns, lb 85.04638 ns, ub 123.1707 ns, ci 0.950

benchmarking naive/fib 20
mean: 120.7269 us, lb 120.5470 us, ub 120.9459 us, ci 0.950
std dev: 1.014556 us, lb 858.6037 ns, ub 1.296920 us, ci 0.950

benchmarking de moivre/fib 10
mean: 7.699219 us, lb 7.671107 us, ub 7.802116 us, ci 0.950
std dev: 247.3021 ns, lb 61.66586 ns, ub 572.1260 ns, ci 0.950
found 4 outliers among 100 samples (4.0%)
  2 (2.0%) high mild
  2 (2.0%) high severe
variance introduced by outliers: 27.726%
variance is moderately inflated by outliers

benchmarking de moivre/fib 20
mean: 8.082639 us, lb 8.018560 us, ub 8.350159 us, ci 0.950
std dev: 595.2161 ns, lb 77.46251 ns, ub 1.408784 us, ci 0.950
found 8 outliers among 100 samples (8.0%)
  4 (4.0%) high mild
  4 (4.0%) high severe
variance introduced by outliers: 67.628%
variance is severely inflated by outliers

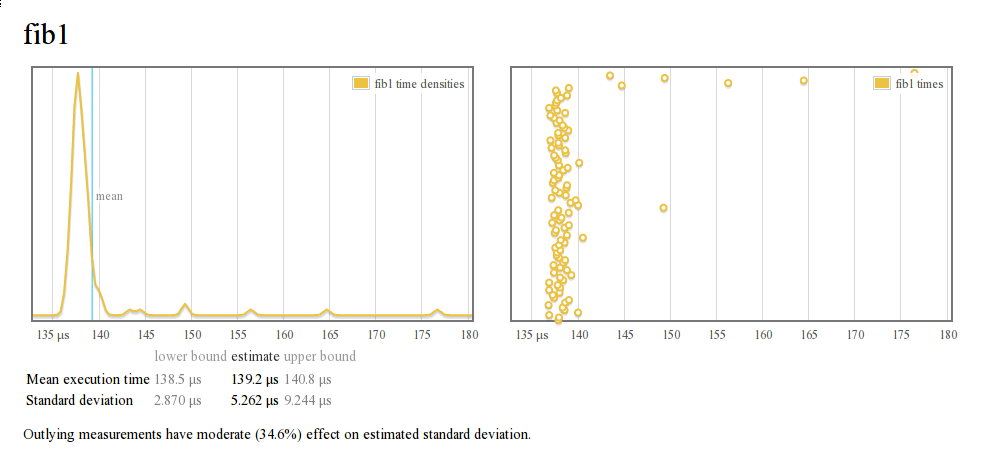
criterion は、ベンチマークの結果をプロットしたものを含む HTML ページを生成することもできます。

$ ghc -O2 --make criterion.hs
$ ./criterion -o bench.html

tasty

Tasty を使えば、テストのフレームワーク全てをまとめて共通の API のもとで扱い、テストの実行可能なバッチを作成して結果を収集することができます。

import Test.Tasty
import Test.Tasty.HUnit
import Test.Tasty.QuickCheck
import qualified Test.Tasty.SmallCheck as SC

arith :: Integer -> Integer -> Property
arith x y = (x > 0) && (y > 0) ==> (x+y)^2 > x^2 + y^2

negation :: Integer -> Bool
negation x = abs (x^2) >= x

suite :: TestTree
suite = testGroup "Test Suite" [
    testGroup "Units"
      [ testCase "Equality" $ True @=? True
      , testCase "Assertion" $ assert $ (length [1,2,3]) == 3
      ],

    testGroup "QuickCheck tests"
      [ testProperty "Quickcheck test" arith
      ],

    testGroup "SmallCheck tests"
      [ SC.testProperty "Negation" negation
      ]
  ]

main :: IO ()
main = defaultMain suite

$ runhaskell TestSuite.hs
Unit tests
  Units
    Equality:        OK
    Assertion:       OK
  QuickCheck tests
    Quickcheck test: OK
      +++ OK, passed 100 tests.
  SmallCheck tests
    Negation:        OK
      11 tests completed