インタプリタ
はじめに
ラムダ計算は、多くの言語で理論と実用における基礎を為しています。全てのラムダ計算の中心には 3 つの構成要素があります。
- Var:変数
- Lam:ラムダ抽象
- App:適用
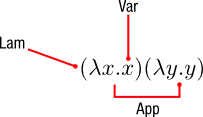
これらの構成をモデル化する方法やデータ構造での表現はいくつもありますが、それらはすべてある程度は 3 つの要素から成っているのです。例えば、String の名前をラムダ束縛子と変数に用いるラムダ計算は以下のように書くことができます。
type Name = String
data Exp
= Var Name
| Lam Name Exp
| App Exp Exp
式の本体に現れる全ての変数が外側のラムダ束縛子により参照されているラムダ式は閉じていると言い、束縛されていない自由変数のある式を開いていると言います。
参照:
HOAS
高階抽象構文(Higher Order Abstract Syntax, HOAS)は、言語の中でラムダ式を実装する際に、ラムダ式の束縛子がホスト言語(即ち Haskell)のラムダ束縛子へと直接変換されるようにするテクニックです。こうして Haskell の実装を活用することで、私たちのカスタム言語に置換の装置をもたらすことができるのです。
{-# LANGUAGE GADTs #-}
data Expr a where
Con :: a -> Expr a
Lam :: (Expr a -> Expr b) -> Expr (a -> b)
App :: Expr (a -> b) -> Expr a -> Expr b
i :: Expr (a -> a)
i = Lam (\x -> x)
k :: Expr (a -> b -> a)
k = Lam (\x -> Lam (\y -> x))
s :: Expr ((a -> b -> c) -> (a -> b) -> (a -> c))
s = Lam (\x -> Lam (\y -> Lam (\z -> App (App x z) (App y z))))
eval :: Expr a -> a
eval (Con v) = v
eval (Lam f) = \x -> eval (f (Con x))
eval (App e1 e2) = (eval e1) (eval e2)
skk :: Expr (a -> a)
skk = App (App s k) k
example :: Integer
example = eval skk 1
-- 1
HOAS の項を整形表示しようとすると、かなりややこしいことになりえます。関数の本体が Haskell のラムダ束縛子の下にあるからです。
PHOAS
PHOAS (Parametric Higher Order Abstract Syntax) と呼ばれる HOAS と少し異なる形式では、束縛子の型を引数に持つラムダのデータ型を使います。この形式では、評価をするにはラムダ式を包むための別個の Value 型へとアンパックする必要があります。
{-# LANGUAGE RankNTypes #-}
data ExprP a
= VarP a
| AppP (ExprP a) (ExprP a)
| LamP (a -> ExprP a)
| LitP Integer
data Value
= VLit Integer
| VFun (Value -> Value)
fromVFun :: Value -> (Value -> Value)
fromVFun val = case val of
VFun f -> f
_ -> error "not a function"
fromVLit :: Value -> Integer
fromVLit val = case val of
VLit n -> n
_ -> error "not a integer"
newtype Expr = Expr { unExpr :: forall a . ExprP a }
eval :: Expr -> Value
eval e = ev (unExpr e) where
ev (LamP f) = VFun(ev . f)
ev (VarP v) = v
ev (AppP e1 e2) = fromVFun (ev e1) (ev e2)
ev (LitP n) = VLit n
i :: ExprP a
i = LamP (\a -> VarP a)
k :: ExprP a
k = LamP (\x -> LamP (\y -> VarP x))
s :: ExprP a
s = LamP (\x -> LamP (\y -> LamP (\z -> AppP (AppP (VarP x) (VarP z)) (AppP (VarP y) (VarP z)))))
skk :: ExprP a
skk = AppP (AppP s k) k
example :: Integer
example = fromVLit $ eval $ Expr (AppP skk (LitP 3))
参照:
完成形インタプリタ
型クラスを使えば完成形インタプリタを実装できます。これは、データコンストラクタでは無く型クラスと結びついた関数を使って、拡張可能な項の集合をモデル化するものです。型クラスのインスタンスはそれらの項に対するインタプリタになっています。
例えば、基本的な算術を含む小さい言語を書いて、その後、私たちの式言語 (expression language) が乗算演算子も使えるように、基盤を変えずに拡張する、ということができます。同時に、私たちのインタプリタの論理は、新しい式を扱えるように拡張しても変わらないままです。
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE TypeSynonymInstances #-}
{-# LANGUAGE NoMonomorphismRestriction #-}
class Expr repr where
lit :: Int -> repr
neg :: repr -> repr
add :: repr -> repr -> repr
mul :: repr -> repr -> repr
instance Expr Int where
lit n = n
neg a = -a
add a b = a + b
mul a b = a * b
instance Expr String where
lit n = show n
neg a = "(-" ++ a ++ ")"
add a b = "(" ++ a ++ " + " ++ b ++ ")"
mul a b = "(" ++ a ++ " * " ++ b ++ ")"
class BoolExpr repr where
eq :: repr -> repr -> repr
tr :: repr
fl :: repr
instance BoolExpr Int where
eq a b = if a == b then tr else fl
tr = 1
fl = 0
instance BoolExpr String where
eq a b = "(" ++ a ++ " == " ++ b ++ ")"
tr = "true"
fl = "false"
eval :: Int -> Int
eval = id
render :: String -> String
render = id
expr :: (BoolExpr repr, Expr repr) => repr
expr = eq (add (lit 1) (lit 2)) (lit 3)
result :: Int
result = eval expr
-- 1
string :: String
string = render expr
-- "((1 + 2) == 3)"
タグ無し完成形インタプリタ
ラムダ計算の評価器を書く場合も、同様に完成形インタプリタと恒等関手 (identity functor) を用いてモデル化することができます。
import Prelude hiding (id)
class Expr rep where
lam :: (rep a -> rep b) -> rep (a -> b)
app :: rep (a -> b) -> (rep a -> rep b)
lit :: a -> rep a
newtype Interpret a = R { reify :: a }
instance Expr Interpret where
lam f = R $ reify . f . R
app f a = R $ reify f $ reify a
lit = R
eval :: Interpret a -> a
eval e = reify e
e1 :: Expr rep => rep Int
e1 = app (lam (\x -> x)) (lit 3)
e2 :: Expr rep => rep Int
e2 = app (lam (\x -> lit 4)) (lam $ \x -> lam $ \y -> y)
example1 :: Int
example1 = eval e1
-- 3
example2 :: Int
example2 = eval e2
-- 4
参照:
データ型
代数的データ型を説明する際に難しい話をごまかすためによくなされるのは、和型、積型、多項式の間にどれほど自然な対応があるかを示すことです。
data Void -- 0
data Unit = Unit -- 1
data Sum a b = Inl a | Inr b -- a + b
data Prod a b = Prod a b -- a * b
type (->) a b = a -> b -- b ^ a
直感的にはこれにより、型に属する値の集合の濃度が必ず穴の数に応じて与えられる、という考えが導けます。積型は積(カルテシアン積の濃度)により、和型は穴の和により、関数型は「終域の数」の「始域の数」乗により、値の個数が決まります。
-- 1 + A
data Maybe a = Nothing | Just a
再帰型は、これらの項の無限の連なりに対応しています。
-- pseudocode
-- μX. 1 + X
data Nat a = Z | S Nat
Nat a = μ a. 1 + a
= 1 + (1 + (1 + ...))
-- μX. 1 + A * X
data List a = Nil | Cons a (List a)
List a = μ a. 1 + a * (List a)
= 1 + a + a^2 + a^3 + a^4 ...
-- μX. A + A*X*X
data Tree a f = Leaf a | Tree a f f
Tree a = μ a. 1 + a * (List a)
= 1 + a^2 + a^4 + a^6 + a^8 ...
参照:
F代数
始代数のアプローチが完成形インタプリタのアプローチと異なるのは、項が代数的データ型として表されていて、インタプリタが再帰を実装していて、パターンマッチにより評価が起こるという点です。
type Algebra f a = f a -> a
type Coalgebra f a = a -> f a
newtype Fix f = Fix { unFix :: f (Fix f) }
cata :: Functor f => Algebra f a -> Fix f -> a
ana :: Functor f => Coalgebra f a -> a -> Fix f
hylo :: Functor f => Algebra f b -> Coalgebra f a -> a -> b
Hasell では F 代数は関手 f a と f a -> a の組み合わせです。余代数は関数を逆にしたものです。任意の関手 f に対して、再帰的な Fix newtype ラッパを使って再帰の巻き込み (rolling)・押し広げ (unrolling) を行うことができます。
newtype Fix f = Fix { unFix :: f (Fix f) }
Fix :: f (Fix f) -> Fix f
unFix :: Fix f -> f (Fix f)
Fix f = f (f (f (f (f (f ( ... ))))))
newtype T b a = T (a -> b)
Fix (T a)
Fix T -> a
(Fix T -> a) -> a
(Fix T -> a) -> a -> a
...
この形式では、データ型に依らない一般性のある畳み込み [folding] / 展開 [unfolding] 関数を、純粋に関手の下で再帰を行うという形で、書いていくことができます。
cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix
ana :: Functor f => Coalgebra f a -> a -> Fix f
ana coalg = Fix . fmap (ana coalg) . coalg
これら二関数はカタモーフィズム (catamorphism) とアナモーフィズム (anamorphism) と言います。特に注目すべきなのは、二関数の型が矢印の方向で単純に逆になっているということです。別の考え方をすれば、二関数は、構造を保存する平らな、f a と a の間の写像を定める代数 / 余代数を、不動点を畳み込む / 展開する関数へと変換するのです。このアプローチが特に優れているのは、再帰が関手の定義の内部へと隠蔽されているため、平らな変換の論理を実装するだけでいいという点です!
この形式で自然数を構成した例:
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE UndecidableInstances #-}
type Algebra f a = f a -> a
type Coalgebra f a = a -> f a
newtype Fix f = Fix { unFix :: f (Fix f) }
-- カタモーフィズム (catamorphism)
cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix
-- アナモーフィズム (anamorphism)
ana :: Functor f => Coalgebra f a -> a -> Fix f
ana coalg = Fix . fmap (ana coalg) . coalg
-- ハイロモーフィズム (hylomorphism)
hylo :: Functor f => Algebra f b -> Coalgebra f a -> a -> b
hylo f g = cata f . ana g
type Nat = Fix NatF
data NatF a = S a | Z deriving (Eq,Show)
instance Functor NatF where
fmap f Z = Z
fmap f (S x) = S (f x)
plus :: Nat -> Nat -> Nat
plus n = cata phi where
phi Z = n
phi (S m) = s m
times :: Nat -> Nat -> Nat
times n = cata phi where
phi Z = z
phi (S m) = plus n m
int :: Nat -> Int
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
nat :: Integer -> Nat
nat = ana (psi Z S) where
psi f _ 0 = f
psi _ f n = f (n-1)
z :: Nat
z = Fix Z
s :: Nat -> Nat
s = Fix . S
type Str = Fix StrF
data StrF x = Cons Char x | Nil
instance Functor StrF where
fmap f (Cons a as) = Cons a (f as)
fmap f Nil = Nil
nil :: Str
nil = Fix Nil
cons :: Char -> Str -> Str
cons x xs = Fix (Cons x xs)
str :: Str -> String
str = cata phi where
phi Nil = []
phi (Cons x xs) = x : xs
str' :: String -> Str
str' = ana (psi Nil Cons) where
psi f _ [] = f
psi _ f (a:as) = f a as
map' :: (Char -> Char) -> Str -> Str
map' f = hylo g unFix
where
g Nil = Fix Nil
g (Cons a x) = Fix $ Cons (f a) x
type Tree a = Fix (TreeF a)
data TreeF a f = Leaf a | Tree a f f deriving (Show)
instance Functor (TreeF a) where
fmap f (Leaf a) = Leaf a
fmap f (Tree a b c) = Tree a (f b) (f c)
depth :: Tree a -> Int
depth = cata phi where
phi (Leaf _) = 0
phi (Tree _ l r) = 1 + max l r
example1 :: Int
example1 = int (plus (nat 125) (nat 25))
-- 150
あるいは、スコープを定める辞書に依存する小さい式言語に対するインタプリタの例:
{-# LANGUAGE GADTs #-}
{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE UndecidableInstances #-}
import Control.Applicative
import qualified Data.Map as M
type Algebra f a = f a -> a
type Coalgebra f a = a -> f a
newtype Fix f = Fix { unFix :: f (Fix f) }
cata :: Functor f => Algebra f a -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix
ana :: Functor f => Coalgebra f a -> a -> Fix f
ana coalg = Fix . fmap (ana coalg) . coalg
hylo :: Functor f => Algebra f b -> Coalgebra f a -> a -> b
hylo f g = cata f . ana g
type Id = String
type Env = M.Map Id Int
type Expr = Fix ExprF
data ExprF a
= Lit Int
| Var Id
| Add a a
| Mul a a
deriving (Show, Eq, Ord, Functor)
deriving instance Eq (f (Fix f)) => Eq (Fix f)
deriving instance Ord (f (Fix f)) => Ord (Fix f)
deriving instance Show (f (Fix f)) => Show (Fix f)
eval :: M.Map Id Int -> Fix ExprF -> Maybe Int
eval env = cata phi where
phi ex = case ex of
Lit c -> pure c
Var i -> M.lookup i env
Add x y -> liftA2 (+) x y
Mul x y -> liftA2 (*) x y
expr :: Expr
expr = Fix (Mul n (Fix (Add x y)))
where
n = Fix (Lit 10)
x = Fix (Var "x")
y = Fix (Var "y")
env :: M.Map Id Int
env = M.fromList [("x", 1), ("y", 2)]
compose :: (f (Fix f) -> c) -> (a -> Fix f) -> a -> c
compose x y = x . unFix . y
example :: Maybe Int
example = eval env expr
-- Just 30
このアプローチが特に優れているのは、カタモーフィズムが合成されると非常に自然に効率的な合成変換になるということです。
compose :: Functor f => (f (Fix f) -> c) -> (a -> Fix f) -> a -> c
compose f g = f . unFix . g
参照:
再帰スキーム
上記のF代数の例で使ったコードは、recursion-schemesという簡単に手に入るライブラリで実装されています。
{-# LANGUAGE TypeFamilies #-}
{-# LANGUAGE DeriveFunctor #-}
import Data.Functor.Foldable
type Var = String
data Exp
= Var Var
| App Exp Exp
| Lam [Var] Exp
deriving Show
data ExpF a
= VarF Var
| AppF a a
| LamF [Var] a
deriving Functor
type instance Base Exp = ExpF
instance Foldable Exp where
project (Var a) = VarF a
project (App a b) = AppF a b
project (Lam a b) = LamF a b
instance Unfoldable Exp where
embed (VarF a) = Var a
embed (AppF a b) = App a b
embed (LamF a b) = Lam a b
fvs :: Exp -> [Var]
fvs = cata phi
where phi (VarF a) = [a]
phi (AppF a b) = a ++ b
phi (LamF a b) = foldr (filter . (/=)) a b
使用例:
{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE KindSignatures #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE TypeSynonymInstances #-}
import Data.Traversable
import Control.Monad hiding (forM_, mapM, sequence)
import Prelude hiding (mapM)
import qualified Data.Map as M
newtype Fix (f :: * -> *) = Fix { outF :: f (Fix f) }
-- カタモーフィズム
cata :: Functor f => (f a -> a) -> Fix f -> a
cata f = f . fmap (cata f) . outF
-- モナディックなカタモーフィズム
cataM :: (Traversable f, Monad m) => (f a -> m a) -> Fix f -> m a
cataM f = f <=< mapM (cataM f) . outF
data ExprF r
= EVar String
| EApp r r
| ELam r r
deriving (Show, Eq, Ord, Functor)
type Expr = Fix ExprF
instance Show (Fix ExprF) where
show (Fix f) = show f
instance Eq (Fix ExprF) where
Fix x == Fix y = x == y
instance Ord (Fix ExprF) where
compare (Fix x) (Fix y) = compare x y
mkApp :: Fix ExprF -> Fix ExprF -> Fix ExprF
mkApp x y = Fix (EApp x y)
mkVar :: String -> Fix ExprF
mkVar x = Fix (EVar x)
mkLam :: Fix ExprF -> Fix ExprF -> Fix ExprF
mkLam x y = Fix (ELam x y)
i :: Fix ExprF
i = mkLam (mkVar "x") (mkVar "x")
k :: Fix ExprF
k = mkLam (mkVar "x") $ mkLam (mkVar "y") $ (mkVar "x")
subst :: M.Map String (ExprF Expr) -> Expr -> Expr
subst env = cata alg where
alg (EVar x) | Just e <- M.lookup x env = Fix e
alg e = Fix e
参照:
hintとmueval
GHC も実際には任意の Haskell ソースをさっと解釈するために、GHC のバイトコード・インタプリタに放り込んでいます(GHCi でも同じものが使われています)。hint パッケージを使えば、任意の文字列を構文解析して Haskell プログラムへと変換し、型検査・評価を行うことができます。
import Language.Haskell.Interpreter
foo :: Interpreter String
foo = eval "(\\x -> x) 1"
example :: IO (Either InterpreterError String)
example = runInterpreter foo
これを基盤としてライブラリを作るのは一般には賢いことではありません。もちろん、プログラムの目的が任意の Haskell コードを評価する(オンラインの Haskell シェルなどようなもの)ことである場合はその限りではありません。
hint と mueval はどちらも実質的に同じ事をします。GHC の API の少し異なる内部機構を基盤に設計されているだけです。
参照: